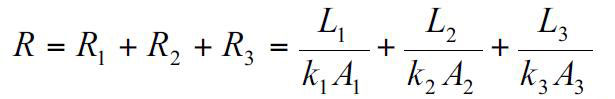مفاهیم پایه انتقال حرارت هدایتی یک بعدی
انتقال حرارتی هدایتی (conduction) که به آن نفوذ نیز می گویند: در انتقال حرارت هدایتی، حرارت از طریق مولکول ها منتقل می شود، این روش انتقال حرارت در جامدات است. یک مثال از این روش انتقال حرارت، انتقال حرارت از یک طرف دیوار (که گرمتر است) به طرف دیگر آن (که دمای کمتری دارد) می باشد.
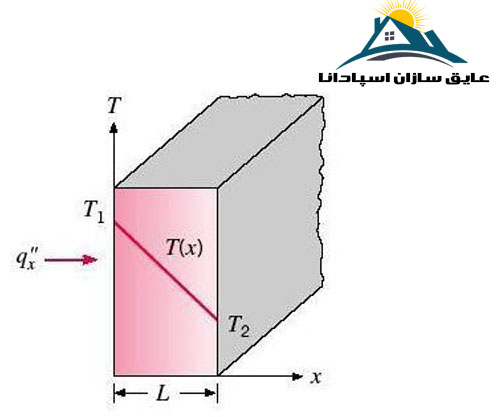
میزان گرمایی که به روش انتقال حرارت هدایتی منتقل می شود به اختلاف دمای دو طرف جسم، خواص فیزیکی و مشخصات هندسی آن بستگی دارد. در شکل زیر شمایی از انتقال حرارت هدایتی در یک جسم جامد آمده است.
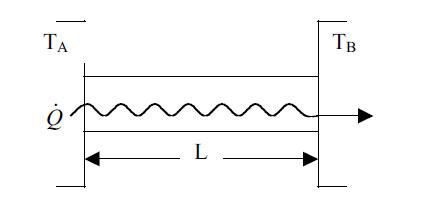
برای یک میله سطح مقطع و طول آن از مشخصات فیزیکی جسم می باشد، هر چقدر که سطح مقطع بزرگتر باشد میزان انتقال حرارت هدایتی در میله نیز بیشتر می شود، همچنین هر چقدر که طول آن بیشتر باشد این میزان کمتر می شود چون حرارت باید مسافت بیشتری را طی کند و با مقاومت بیشتری روبه رو می شود.
یکی دیگر از عواملی که بر انتقال حرارت هدایتی تاثیر می گذارد اختلاف دمای بین دو سطح جسم است به طوری که هرچقدر این مقدار بیشتر باشد نرخ انتقال حرارت نیز افزایش می یابد و اگر دو سطح جسم همدما باشند (TA = TB) انتقال حرارتی وجود ندارد.
با توجه به مطالب بالا، رابطه انتقال حرارت هدایت یک بعدی بین دو سطح با طول و خواص فیزیکی معین، از رابطه زیر بدست می آید.
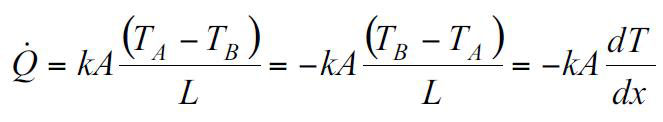
که در این رابطه Q نرخ انتقال حرارت هدایتی یک بعدی، A سطح مقطع جسم، L طول آن و k ضریب انتقال حرارت هدایتی است و خاصیت فیزیکی ماده می باشد.
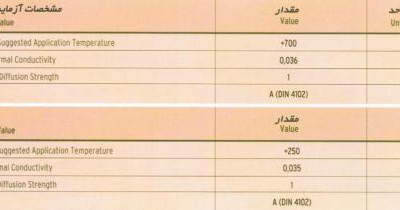
اصلی ترین پارامتر در مواد عایق حرارتی همین ضریب انتقال حرارت هدایتی است که هر چقدر این مقدار کمتر باشد عایق حرارتی عملکرد بهتری دارد. واحد آن وات بر متر بر کلوین (W/m.K) می باشد.
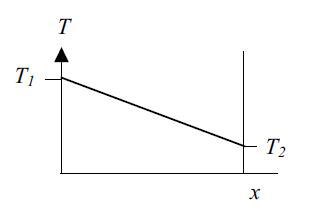
اگر نرخ انتقال حرارت را بر سطح تقسیم کنیم پارامتر دیگری بدست می آید به نام شار حرارتی که این پارامتر نیز در محاسبات انتقال حرارت به روش هدایت مهم می باشد و از رابطه ی پایین بدست می آید:
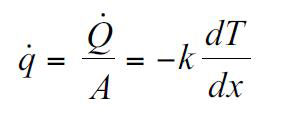
فرمول بالا اهمیت بدست آوردن رابطه بین دما و طول (dT/dx) را در محاسبه انتقال حرارت نشان می دهد.
رابطه بین دما و طول در انتقال حرارت هدایتی یک بعدی در حالت پایا
با توجه به شرایط مرزی حاکم بر مسئله و با فرض اینکه انتقال حرارت بصورت یک بعدی (فقط در راستای طول جسم جامد) صورت می گیرد، می توان رابطه بین دما و طول را بدست آورد.
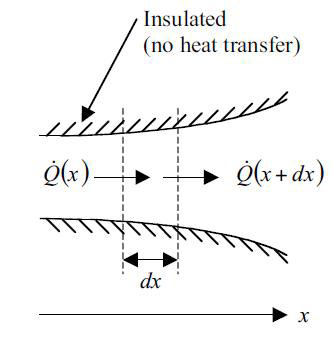
رابطه بین دما و طول در حالت پایا در انتقال حرارت هدایتی یک بعدی بصورت زیر است:
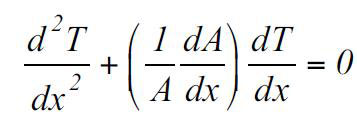
مثال: دیواری به ضخامت L که دمای دو طرف آن T1 و T2 است را در نظر بگیرید.
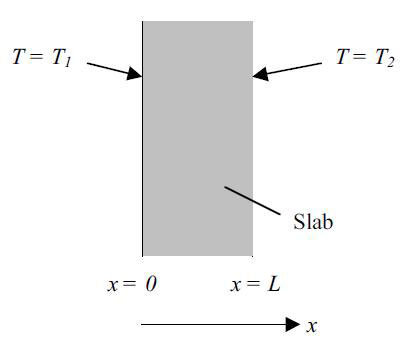
در مثال بالا سطح ثابت است و در راستای x تغییر نمی کند بنابراین dA/dx=0 می شود و رابطه ی بالا به صورت زیر ساده می شود:
با انتگرال گیری از رابطه ی بالا داریم: T(x)=ax+b که a و b را می توان با توجه به شرایط مرزی بدست آورد. یعنی T(0)=T1 و T(L)=T2
در نتیجه رابطه بالا بصورت زیر در می آید:
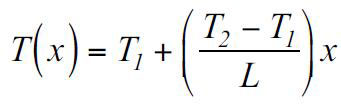
و رابطه ی شار حرارتی در واحد سطح بصورت زیر محاسبه می شود که یک مقدار ثابت است.
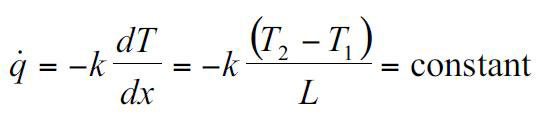
نمودار زیر روند تغییرات دما در طول دیوار را نشان می دهد.
این سوال مطرح است که فرض شرایط پایا و انتقال حرارت یک بعدی چقدر می تواند در عایق کاری و حل مسائل واقعی درست باشد و چقدر می توان به آن اطمینان کرد؟ جواب این است که در حالت کلی نمی توان فرض حالت پایا و انتقال حرارت یک بعدی را بطور 100% تایید کرد اما در صورتی که سطح بسیار بزرگتر از طول مسیر انتقال حرارت (ضخامت دیوار) باشد، فرض حالت پایا و انتقال حرارت یک بعدی تا حد زیادی درست است و می توان به نتایج بدست آمده برای حل مسائل عایق کاری واقعی اطمینان حاصل کرد.
مقاومت حرارتی
مسائل انتقال حرارت را می توان بصورت سمبلیک به مسائل مدارهای الکتریکی تشبیه کرد. این روش باعث آسان تر شدن حل مسائل انتقال حرارت در عایق کاری می شود. در این تشابه نرخ انتقال حرارت Q مشابه آمپر و اختلاف دما (T1-T2) به جای ولتاژ در نظر گرفته می شود.
با توجه به رابطه V=RI در مدارهای الکتریکی رابطه انتقال حرارت بصورت زیر بدست می آید:
Q=(T1 – T2)/R
و با توجه به رابطه انتقال حرارت که در بالا بدست آمده، می توان نتیجه گرفت که مقاومت حرارتی (R) برابر است با:
R=L/kA
که L ضخامت جسم، A سطح مقطع آن و k ضریب انتقال حرارت هدایتی جسم است.
این شبیه سازی مقاومت حرارتی با مدارهای الکتریکی و تعریف عبارت مقاومت حرارتی می توان کمک زیادی در حل مسائل انتقال حرارت بکند. برای مثال شکل زیر را در نظر بگیرید که از دو ماده با جنس های مختلف ساخته شده است.
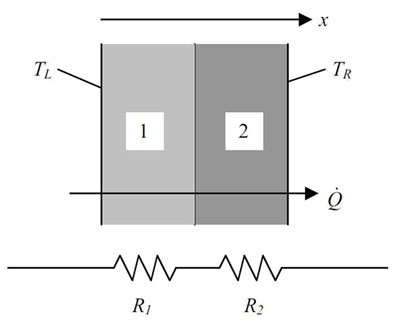
مانند مدارهای الکتریکی که مقاومت های سری با هم جمع می شوند در این مسئله انتقال حرارت نیز مقاومت های حرارتی دو جسم با جنس مختلف با هم جمع می شود و مقاومت حرارتی کلی از رابطه زیر بدست می آید:
R=R1+R2
بنابراین نرخ انتقال حرارت برابر است با:

مثال: سطح عایقی را در نظر بگیرید که بوسیله ی یک پیچ به دیوار متصل شده است:
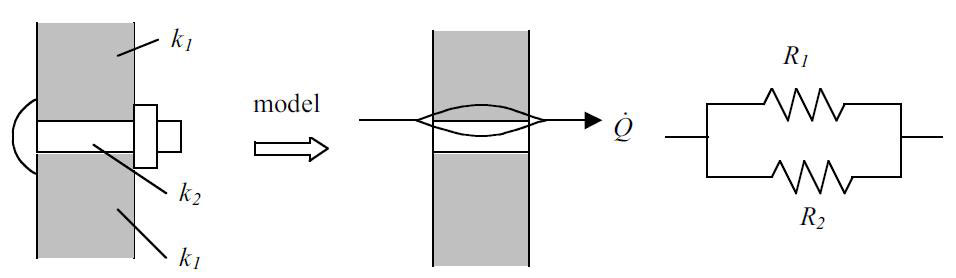
در این حالت مقاومت های حرارتی بصورت موازی هستند و مقاومت کلی از رابطه زیر بدست می آید:
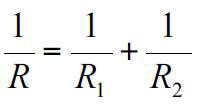
همچنین نرخ انتقال حرارت هدایتی کل برابر با مجموع نرخ انتقال حرارت از دیوار و پیچ است:
Q=Q1+Q2
مثال: دیوار آجری را در نظر بگیرید که در دو طرف آن عایق حرارتی قرار داشته باشد. مقاومت کلی آن برابر با جمع سه مقاومت سری است.
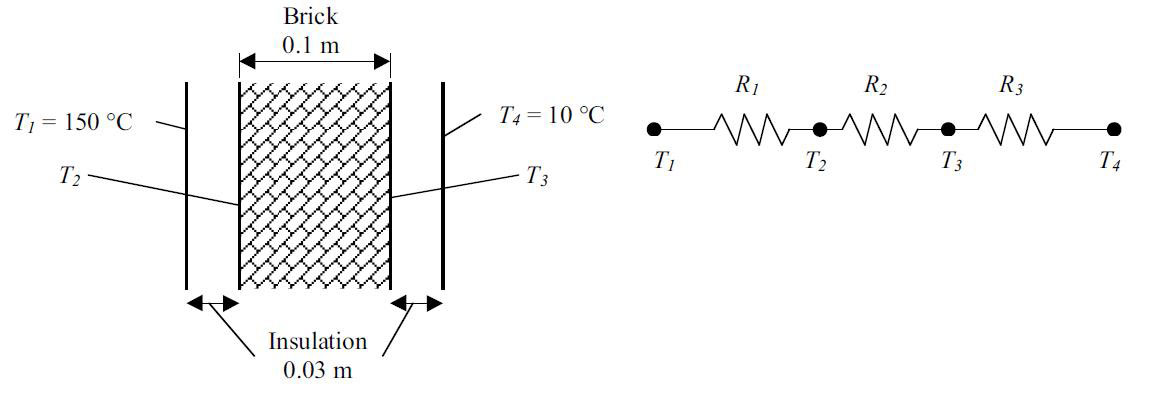
ضریب کلی انتقال حرارت برابر است با: