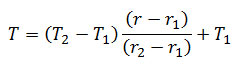مفاهیم پایه انتقال حرارت یک بعدی استوانه ای

عایق کاری حرارتی لوله ها و نیم لوله های از اهمیت به سزایی برخوردار است، چه در صنایع و چه در عایق کاری لوله های ساختمان، بنابراین شناخت نحوه ی انتقال حرارت در لوله ها برای فعالان در این عرصه اهمیت ویژه دارد.
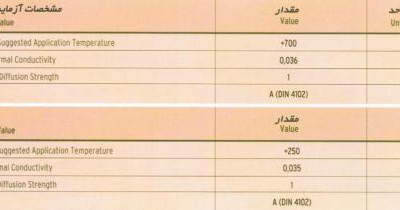
عایق های حرارتی لوله ای بصورت پیش ساخته در سایزها، ضخامت ها و چگالی های مختلف تولید می شوند. از جمله این نوع عایق ها می توان به عایق های لوله ای پش ساخته پشم های معدنی (مانند پشم سنگ) اشاره کرد.
به منظور عایق کاری لوله ها و نیم لوله ها استفاده از مختصات کارتزین امکان پذیر است اما به دلیل پیچیدگی ها آن استفاده از مختصات قطبی بسیار آسان تر می باشد و باعث سهولت در محاسبات می گردد. برای ساده تر شدن محاسبات در مختصات قطبی می توان انتقال حرارت در لوله ها را تنها در جهت شعاع آن ها و بصورت یک بعدی در نظر گرفت.
شکل زیر شماتیکی از عایق های حرارتی لوله ای است:
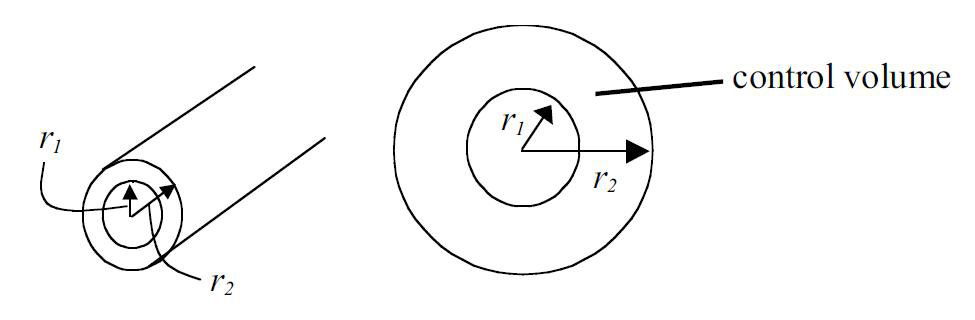
با فرض یک بعدی بودن انتقال حرارت، دما در راستای شعاع تغییر می کند. در این حالت می توان معادله تغییرات دما را بر حسب شعاع بصورت زیر بیان کرد:
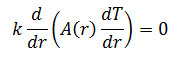
با حل معادله بالا، رابطه دما با شعاع به صورت زیر در می آید، دما در داخل لوله T1 و در سطح آن T2 در نظر گرفته شده است:
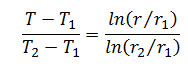
نرخ انتقال حرارت
نرخ انتقال حرارت در مختصات استوانه ای از رابطه زیر بدست می آید:
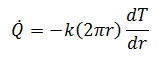
با توجه به این رابطه و رابطه ی بالا، معادله زیر برای نرخ انتقال حرارت بدست می آید:
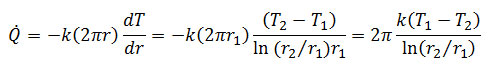
با توجه به رابطه بالا مقاومت حرارتی در مختصات استوانه ای از رابطه بالا بدست می آید:
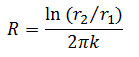
و نرخ انتقال حرارت برابر می شود با:
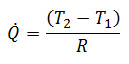
در حالتی که ضخامت عایق حرارتی استفاده شده بسیار کم باشد (یعنی شعاع لوله خیلی بیشتر از ضخامت عایق است)، معادله از حالت لگاریتم خارج می شود و می توان آن را به شکل زیر ساده کرد: